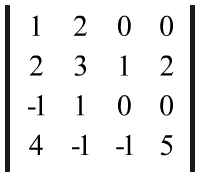Абакумова 2013 АГАУ ЭкономФак
Абакумова Н. А., Зенков А. В., Кокшарова М. В., Кулешова И. Г., Морозова С. В., Павлов Г. А., Прусакова Г. В., Цымбалист О. В.
Методические указания и контрольные задания по математике для студентов-заочников АГАУ
Барнаул: Изд-во АГАУ, 2013
ДЛЯ ЭКОНОМИЧЕСКОГО ФАКУЛЬТЕТА
Представлено решенных задач: 69 из 200 (35%). Пополнение производится регулярно.
Остальные Вы можете заказать у нас на льготных условиях! Недорого, быстро и качественно! Оформить заказ
| Наименование | Задание | Тип | Цена | |
|---|---|---|---|---|
| Вариант №051 |
Даны векторы a = 2i – j , b = {–1, 3, 5}, c = 4i – 2j . Определить вектор x , удовлетворяющий следующим условиям: 1) x ⊥ b ; 2) x c = 0; 3) x a = 3. Определить объем треугольной пирамиды ABCD A(3, –5, –2), B(–4, 2, 3), C(1, 5, 7), D(–2, –4, 5).
|
Задача | 90 ₽ | |
| Вариант №009 |
|
Задача | 90 ₽ | |
| Вариант №043 |
При каком значении α векторы a = 2i + αj + 2k , b = i + 2j – 3k , c = 3i – 4j + 7k компланарны? Определить длину вектора a = p + 2q , если |p | = 1, |q | = √3 и ∠(p , q ) = π/6.
|
Задача | 90 ₽ | |
| Вариант №143 |
|
Задача | 90 ₽ | |
| Вариант №106 |
1.
|
Задача | 90 ₽ | |
| Вариант №076 |
1) y = e3x + 4√x3; 2)
|
Задача | 90 ₽ | |
| Вариант №013 |
|
Задача | 90 ₽ | |
| Вариант №064 |
1)
|
Задача | 90 ₽ | |
| Вариант №049 |
Заданы векторы a = –i + 3j + 2k и b = 2i – 3j – 4k . Найти координаты вектора a × b . Определить объем треугольной пирамиды ABCD A(3, –2, 6), B(–6, –2, 3), C(1, 1, –4), D(4, 6, –7). |
Задача | 90 ₽ | |
| Вариант №004 |
|
Задача | 90 ₽ |


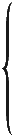 x1 + x2 + x3 + x4 = 1,
x1 + x2 + x3 + x4 = 1, ;
;  ;
;  ;
; 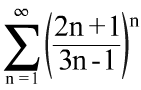 .
.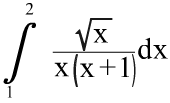 ; 2. y = lnx, y = 0, x = e.
; 2. y = lnx, y = 0, x = e.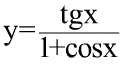 ; 3) y = arcsin(lnx); 4) y = (ex – 1)x.
; 3) y = arcsin(lnx); 4) y = (ex – 1)x.
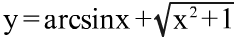 ; 2)
; 2)  ; 3) y = 1/2 sinx2; 4) y = x√x.
; 3) y = 1/2 sinx2; 4) y = x√x.